Laser Inertial Confinement Fusion (ICF)

Jacob Shin

11/11/2022

Dr. Oct

  • Two lighter nuclei combine and form a heavier, more stable nuclei
  • Releases a lot of energy
E=Δmc2
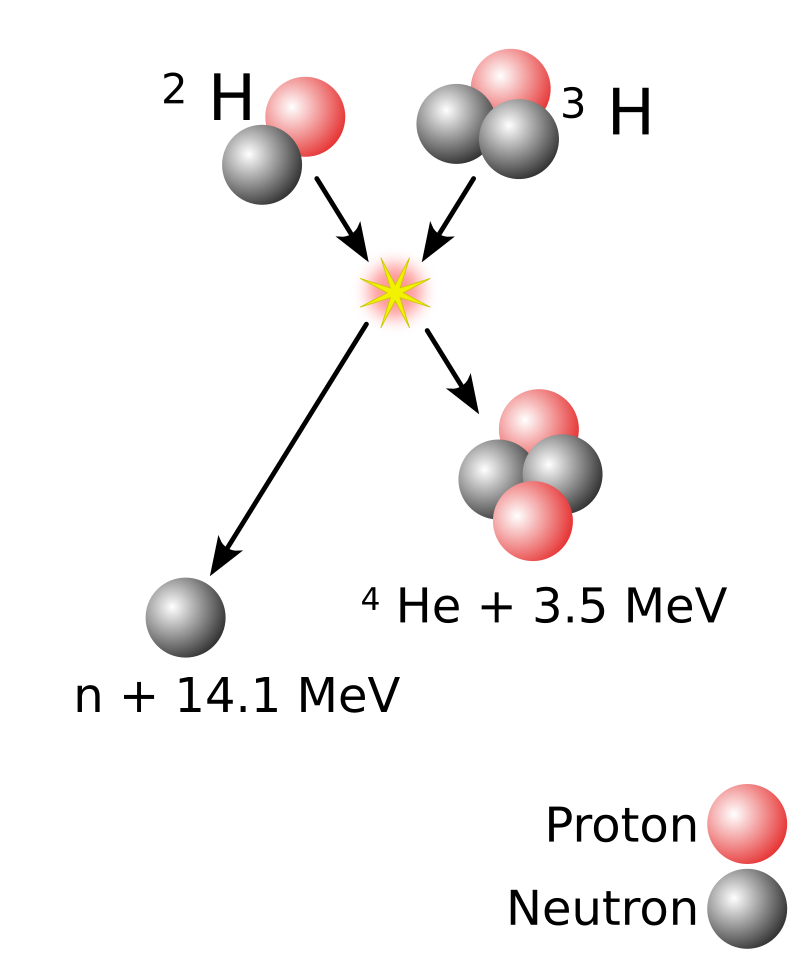Binding Energy Curve Binding Energy Curve

Ways of doing Fusion

  • The two nuceli must overcome colomb repulsion before the strong force kicks in
  • This means you have some force that confines the nuclei
Gravity Sun Magnets ITER Lasers NIF
  • In order for a fusion reactor to be useful, it has to produce more energy than what we put in:
Q=Energy Released by FusionInput Energy
Qfuel=Energy Released by FusionEnergy Absorbed by Fuel

Lawson Criteria/Triple Product

nTτE≥3T2(fc+Q−1fuel)⟨σv⟩ϵf/4−CB√T

  • While running a fusion reactor, some of the energy is lost
  • n is the density of the fuel
  • T is the temperature of the fuel
  • τE is the confinement time, which tells you how long to keep the fuel confined together
  • v is the fuel particles' velocity
  • fc, σ, CB, η, ϵF are all constants that depends on the fuel
In [41]:
from IPython.display import HTML; HTML('<blockquote class="twitter-tweet"><p lang="en" dir="ltr">&quot;Progress toward fusion energy breakeven and gain as measured against the Lawson criterion&quot; by <a href="https://twitter.com/ScottCHsu?ref_src=twsrc%5Etfw">@ScottCHsu</a> and myself is published (open access)! GIF of achieved Lawson parameter vs temperature below shows the progress. <a href="https://t.co/VKFM1XubXR">https://t.co/VKFM1XubXR</a> <a href="https://twitter.com/hashtag/fusionenergy?src=hash&amp;ref_src=twsrc%5Etfw">#fusionenergy</a> <a href="https://twitter.com/ARPAE?ref_src=twsrc%5Etfw">@ARPAE</a> <a href="https://twitter.com/AIP_Publishing?ref_src=twsrc%5Etfw">@AIP_Publishing</a> <a href="https://t.co/P1oNjLB8ZN">pic.twitter.com/P1oNjLB8ZN</a></p>&mdash; Sam Wurzel (@swurzel) <a href="https://twitter.com/swurzel/status/1534556521744457731?ref_src=twsrc%5Etfw">June 8, 2022</a></blockquote> <script async src="https://platform.twitter.com/widgets.js" charset="utf-8"></script> ')
Out[41]:

ICF

Laser ICF Laser ICF

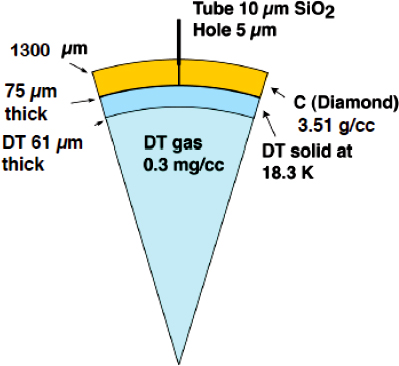
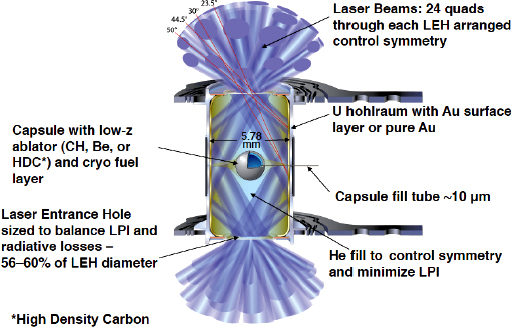
Direct Drive vs. Indirect Drive

Different ICF methods
  • Direct Drive is 8% efficient, but harder to get spherical symmetry
  • Indirect Drive is only 4% efficient, allows for more symmetric implosion and less instabilities

PdV=TdS−dU
Different ICF methods Different ICF methods

Source: https://en.wikipedia.org/wiki/National_Ignition_Facility#/media/File:NIF_building_layout.png

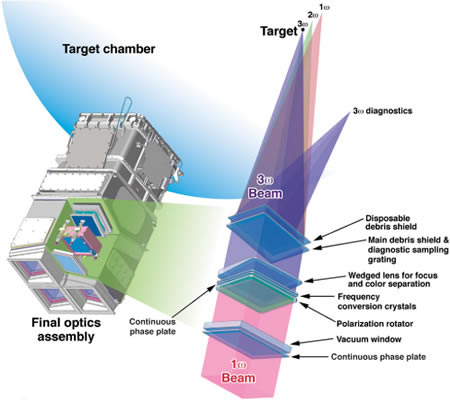
National Ignition Facility (NIF): World's Largest Laser

Capacitance = 0.290 farads
Operating Voltage = 24 kV
Peak Discharge Current = 25 kA
400 megajoules—the world's largest capacitor bank
3,840 high-voltage capacitors

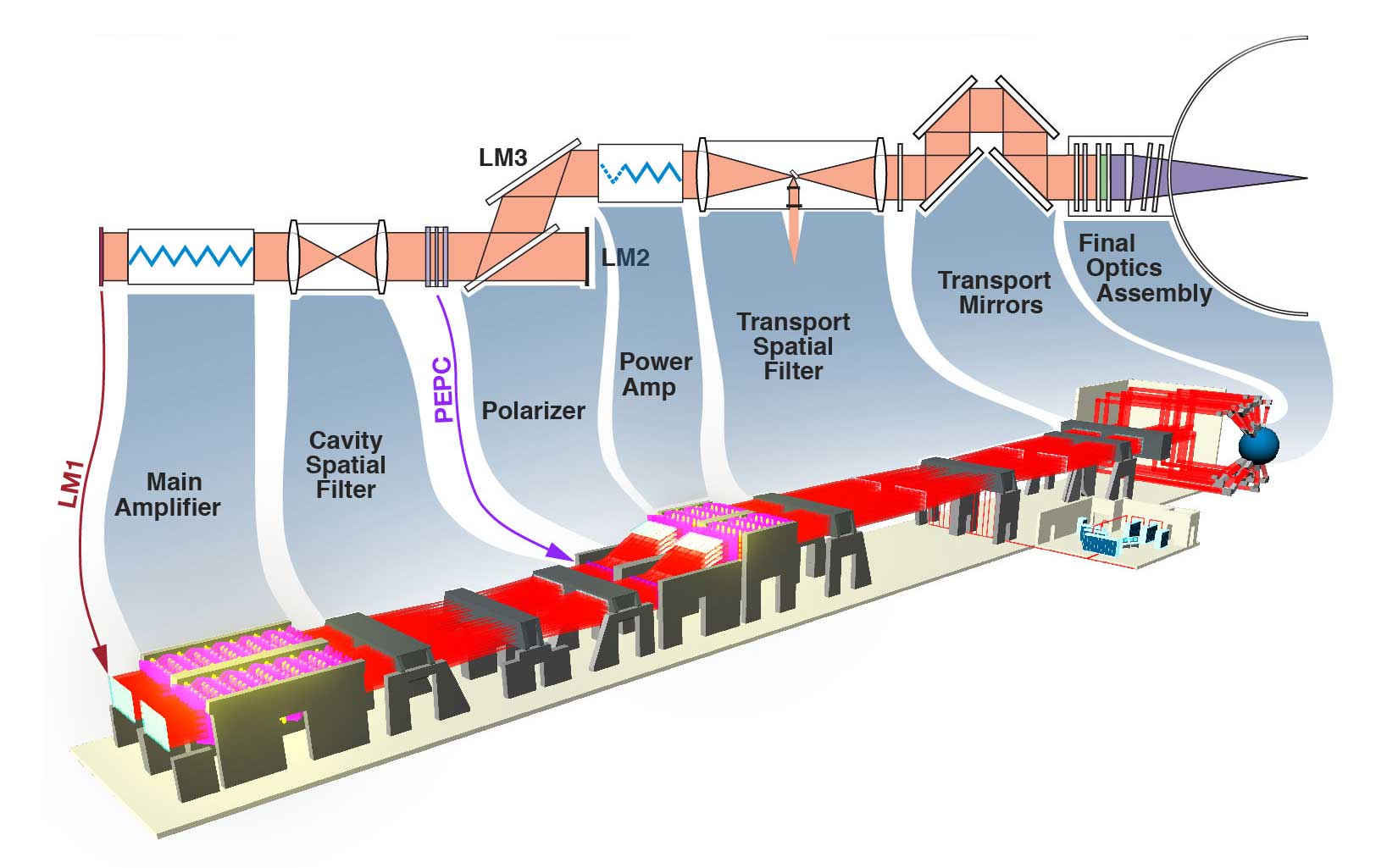
Source: https://lasers.llnl.gov/content/assets/images/about/

Pockell Cell, Main Amplifier, and Polarizer

  • KDP (Potassium Diphosphate) is birefringent -- has two different indices of refraction

  • KDP experiences Pockell's Effect

    • If an electric field is applied to the crystal, the index of refraction changes |Δn|=r2n30E

      where r is the an electro-optical coefficient for KDP and n0 is the initial index of refraction at E=0, and Δn is the change in index of refraction

  • Plasmas are ionized gases - highly conductive due to the free electrons present

  • Density of electrons, ne, determines reflectivity ωp=2πfp=√nee2ϵ0me

  • When the frequency of incoming light, fi, is greater than the plasma frequency, then there is transmission of the light through the plasma fi>fp

This explains why AM radio waves bounce off of the ionosphere (ne≈1011), why metals are reflective and shiny (ne≈1028), and why the surface of the sun isn't shiny (ne≈1020), and why helium plasma is used for the Pockell cell (ne≈1018)

  • ne=1012 cm−3=1018m−3, e=1.6×10−19 C, me=9.10×10−31 kg, ϵ0=8.85×10−12
  • λi=1053 nm
fp=12π√1018⋅(1.6×10−19)28.85×10−12⋅9.10×10−31=8.9 GHz
fi=cλi=285 THz

Thus fi>>fp means the laser will be transmitted through the helium plasma

Second Harmonic Generation

P2=ϵ0χ2E2
E=E0cosωt
⟹P2=ϵ0χ2E20cos2ωt=ϵ0χ2ϵ20(12(1+cos2ωt))

Using double angle formulas, we get the following:

P2=12ϵ0χ2E20+12ϵ0χ2E20cos2ωt

KDP

Spatial Filters

Why is Fusion Hard?

  • Instabilities/Turbulence: Rayleigh Taylor, Kelvin-Helmholtz, Richtmyer–Meshkov, Wakes
  • Scattering: Laser light entering the hohlrahm gets scattered (absorbed by electrons and gold plasma), which reduces the energy that reaches the fuel
    • Stimulated Raman Scattering (SRS)
    • Stimulated Brillouin Scattering (SBS)

Raman Scattering

  • (Spontaneous) Incoming laser photon scatters inelastically
    • The photon from the laser (called a pump photon) is inelastically scattered with some energy transferred into vibrational energy in the molecule
    • The remaining photon has a lower energy (lower frequency) -- Called the stoke's photon
  • (Stimluated) Some of the stoke's photons emitted from spontaneous Raman scattering act as seed photons
    • Pump photon + stokes photons interact with molecules and cause vibrations

Wakes

  • Wakes can be used for particle accelerators!
  • Wakefield: 1GeV with only 3.3 cm, SLAC: 64 meters
In [48]:
import matplotlib.pyplot as plt
%matplotlib notebook
import happi; S=happi.Open(); Rho = S.Field.Field0("-Rho",cmap="Blues_r",vmax=0.01); Env_E = S.Field.Field0("Env_E_abs",cmap="hot",vmin=1,transparent="under")

Loaded simulation '.'
Scanning for Scalar diagnostics
Scanning for Field diagnostics
Scanning for Probe diagnostics
Scanning for ParticleBinning diagnostics
Scanning for RadiationSpectrum diagnostics
Scanning for Performance diagnostics
Scanning for Screen diagnostics
Scanning for Tracked particle diagnostics
In [49]:
happi.multiSlide(Rho,Env_E)
In [46]:
from IPython.display import IFrame
IFrame('./eScholarship UC item 5wb109v8.pdf', width=1200, height=600)
Out[46]:

Image Credits

Sources and Further Reading

In [ ]: